Genetic Algorithms |
|---|
|
Given the series of issues presented above, the following question becomes important: How can we design a NN to learn some aspect of language as well as possible, when we have a high number of variables, and we do not fully understand how these variables interact with each other?
Genetic algorithms are especially well suited for the type of problem where the interaction between variables is not completely understood. The basic principle is to have a population of elements, each of which represents a possible solution. The free variables in each possible solution are represented by a string of numeric values. The genotype of one of these elements is constituted by a particular solution to the problem, as defined when each of the different free variables is assigned a specific value. Each free variable is then known as a gene. The fitness of each of the solutions is measured in terms of how well it can solve a particular problem. Once we know how well each member of the population solves the problem at hand, we combine separate elements of the population to form new solutions. These new solutions also get evaluated based on their ability to solve the problem. The size of the population is maintained constant; only the best elements fitnesswise remain in the population. In this way, the population as a whole tends to move towards better solutions, while at the same time we continuously generate new (possibly better) solutions by combining solutions that have been successful previously. For example, imagine that we have a function that takes six characters as input, and returns an integer as output. We would like to find what combination of six letters will return the highest value, but we have no idea of what function might be computed, or what the relationship between the letters is. If we are working with the English alphabet, we would have 266 possible combinations. Therefore, performing an extensive search would be too expensive. |
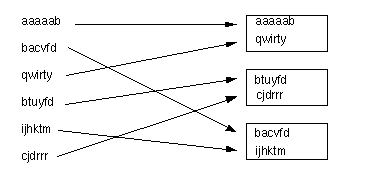
 An initial population, with an example of how they could be paired-up. |
Instead, we can start with an initial population of six random "words" of six characters each, where the fact that we start with six elements in the population has been determined arbitrarily. The fitness of each of these elements is determined using the same function we are trying to optimize. Once we know what the fitness for each of this elements is, we pair them up in some random way. Having paired them up, we proceed to perform a crossover operation to each pair. |
| A crossover point is randomly chosen. From this crossover we will create two new elements, sometimes called offsprings or children. The two new elements will be formed by joining the "head " of one parent with the tail of the other, and vice-versa. Now the two new elements get evaluated for their fitness. Once all pairs in the initial population are subject to the crossover operation, we will have twelve elements, six "parents" and six "children". These twelve elements compete for the six available slots in the population. We will keep the elements with the six best fitness values. |  example of a crossover operation |
| At this point we could perform a random mutation on one or more of the elements. With a low probability we will flip one of the genes of the element, say from a a to c. This operation gives the algorithm a chance to introduce elements into the population that would not have appeared by combining existing elements. While crossover and fitness rewards exploiting those factors found to be positive, mutation rewards the exploring of new possibilities, thus avoiding early convergence into non-optimal solutions. The process now gets repeated for a fixed number of generations, or until we find an element with a fitness of X, or until the average fitness does not change by more than n%, or some other halting criterion.
|
 Back to the Table of Content
Back to the Table of Content