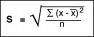You probably found when reading the research article
we discussed in class, that the graphs and descriptions of data used
some symbols that you might not be familiar with. Some of the numbers
were followed by a little plus/minus sign with a smaller number after
that. Sometimes they talked about p-values and ANOVA's
and t-tests.
The idea of all this odd language is just to tell you
something about how the data are distributed. For instance, say we found
out that the average height of people in our class was 60 inches. What
would that tell someone who never saw us about what our class looks
like? Would they think everyone was just about 60 inches tall? Would
they think that half of us were 40" and the other half were 70"? Or
maybe most people were 55" and a few were 52"? How could they tell the
difference? What else would they need to know?
Well some of those symbols you see in the papers are
statistical ways of telling you a little more about the make-up of the
population than just knowing the average. As Le and Boen (1995, p. 104)
put it, "Statistical inference is the procedure whereby inferences about
a population are made on the basis of results obtained from a sample
drawn from that population."
Measures of Central Tendency
The first thing to think about is what kind of "average"
is this? When we say "average," a statistician says "measure of central
tendency." There are three things people can mean when they talk about
central tendency.
1. MEAN is the one most of us mean when we
say "average." It's the sum of all the values in the set divided
by the number of values.
2. MEDIAN is the middle value of all the numbers
in the set (half are bigger, half are smaller)
3. MODE is the value that occurs most often.
Measures of variability
RANGE tells what the largest and smallest values
of the set are.
STANDARD DEVIATION gives a more accurate indication
of how broadly scattered all the values are--not just the largest and
smallest. It is calculated by the following formula
Student t-test is used when you are
comparing two means of populations that have normal distributions.
ANOVA is
a category of test for variance used when you are comparing more
than 2 variables.
It stands for ANalysis Of
VAriance.
Statistical tests are often used to ask whether
two or more means are really different from one another. For instance,
say you think that people who eat vegetarian diets are likely to
be shorter than people who include meat in their diets. So you decide
to compare the heights of a group of vegetarians at
Hampshire and
a group of carnivores, and you calculate the mean height of each
group. (Of course, you'd want to know more about possible differences
between these groups like how long they had followed these diets
and other information about medical and family histories, and maybe
something about their activity levels and details of their diets,
but for now, let's assume you've controlled for these factors.)
If the mean heights of the two groups were exactly
the same, then you might feel comfortable saying that for this population
of people, there appears to be no influence of their current diet on
their height. But what if there was a little difference, like 1/4" difference
in the means? Would you say "Wow, I proved that diets containing meat
make people grow taller!!" Maybe, but that would probably be rash. You'd
want to know more about the data:
• How many subjects were in each
group? Maybe you had so few subjects that the height of one meat
eater who was extremely tall was mainly responsible for causing
the mean of that group to be higher than the vegetarian group.
• What's the standard deviation?
Maybe the range of heights in both groups was so broad that many
or even most of the vegetarians and carnivores were actually the
same heights and it was just a few people at the extreme ends who
contributed to the difference in the means (you might want to learn
more about those people though).
• You might be more convinced if
the difference between the means was 1/2" or 1" or 2". If the difference
between the means was 12", you'd really start thinking you've
got some results that support your hypothesis. But when is the difference
big enough to consider it a "real" difference?
A statistical test is a way of helping you talk
about how significant these differences between the means are. It gives
a standard to test against. If your hypothesis is that the variable
you're looking at (diet) probably doesn't really influence the outcome
(height), then you'll expect no "real" difference between the means.
In statistics talk that's called the "null hypothesis." It means
that your hypothesis is "nothing is happening that is related to the
variable I'm testing."
If you could do a statistical test that would
help you decide that the data you collected cause you to reject your
null hypothesis, that means you've found a statistically significant
difference between the two means. In other words, you have rejected
the idea that nothing is happening, so something is probably happening.
Such a test would show that the difference you see between the means
is probably a "real difference." It sounds like a backwards way to show
you see a real difference by saying you can't prove there is no difference,
but it makes sense when you think about it.
So how do you figure out if you've rejected your
null hypothesis? You do this by figuring out the LEVEL OF SIGNIFICANCE
(or as you've seen it in the article you're reading, the p-value). This
number takes into consideration the difference between the MEANS,
the NUMBER of items that went into calculating each mean, and
the size of the STANDARD DEVIATIONS. The answers generally come
out as small decimals, fractions of 100. So if a p-value comes out to
be 0.05, that means there was a 0.05 (5%) chance that the two means
you were comparing are the same--or a 95% chance that they are
different. The smaller the p-value, the likelier (or higher the probability)
that the difference is "real." A p-value of 0.01 means there was a 1%
chance the two means you were comparing are the same or a 99% chance
they were different!
There's an arbitrary standard people use for
what they call a SIGNIFICANT difference. If a p-value is less
than 0.05, the difference between the means is said to be a STATISTICALLY
SIGNIFICANT difference. In fact, in a scientific paper, if the word
"significant" is used, it has to mean that a statistical test was done
that showed the p-value to be less than 0.05. Now in real life if you're
doing an experiment and the p-value comes out to be 0.06, you don't
throw out the whole idea that there's a difference between the means.
You repeat your experiment with better controls or more subjects. What
you can't do is remove the measurement for that one person who
you think threw the mean off and then recalculate the mean. (You can
do that in the privacy of your own office just to reassure yourself
that it was this data point that messed up your hypothesis, but then
you have to throw those calculations out, report what you did find,
and plan a follow-up study to resolve the question.)
The kind of test you do to see whether there
is a significant difference between the means of two sets of data is
called a t-test. There are several types of t-tests depending
on the way you are comparing data. Basically they just compare the difference
between the means, the standard deviations, and the number of items
of each group you're measuring and give a probability that the means
are statistically different. You use the "t" value to determine the
p-value.
The ANOVA is another test for whether the means
of two groups are "really" different. It acts like a t-test,
but you can use it for 2 or 3 or more groups, and you can analyze more
than one factor at once. For instance you can compare women vs. men
AND veggies vs. meat-eaters both at once. It does this test by looking
at the variance within each group compared to the differences between
groups and the variance of the data as a whole--that's why it's an "analysis
of variance."
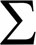 signifies
taking the sum of all those squared differences.
signifies
taking the sum of all those squared differences.